Metriks adalah kumpulan bilangan berbentuk persegi panjang yang disusun menurut
baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut
dengan elemen atau anggota matriks. Dengan representasi matriks, perhitungan
dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam
menjelaskan persamaan linier, transformasi koordinat, dan lainnya. Matriks
seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah,
dikurangkan dan didekomposisikan.
Kamis, 29 Mei 2014
Rabu, 28 Mei 2014
- Bentuk Pangkat
Bentuk-bentuk bilangan seperti 10-11, 1024 , 1022 dan 108 merupakan bentuk-bentuk bilangan berpangkat yang telah anda pelajari saat SMP/MTs. Bentuk-bentuk bilangan berpangkat dapat kita bagi menjadi empat jenis, yaitu: bilangan berpangkat positif, berpangkat nol, berpangkat negatif dan bilangan berpangkat pecahan. Bilangan berpangkat positif, nol dan negatif akan kita pelajari pada sub bab ini sedangkan yang berpangkat pecahan akan kita pelajari pada sub bab berikutnya.
- Bentuk Pangkat
Bentuk-bentuk bilangan seperti 10-11, 1024 , 1022 dan 108 merupakan bentuk-bentuk bilangan berpangkat yang telah anda pelajari saat SMP/MTs. Bentuk-bentuk bilangan berpangkat dapat kita bagi menjadi empat jenis, yaitu: bilangan berpangkat positif, berpangkat nol, berpangkat negatif dan bilangan berpangkat pecahan. Bilangan berpangkat positif, nol dan negatif akan kita pelajari pada sub bab ini sedangkan yang berpangkat pecahan akan kita pelajari pada sub bab berikutnya.
Senin, 26 Mei 2014
1. FILSAFAT
Kata falsafah atau filsafat dalam bahasa Indonesia merupakan kata serapan dari bahasa Arabفلسفة, yang juga diambil dari bahasa Yunani; Φιλοσοφία philosophia.Dalam bahasa ini, kata ini merupakan kata majemuk dan berasal dari kata-kata (philia= persahabatan, cinta dsb.) dan (sophia = "kebijaksanaan").Sehingga arti harafiahnya adalah seorang “pencinta kebijaksanaan”. Kata filosofi yang dipungut dari bahasa Belanda juga dikenal di Indonesia.Bentuk terakhir ini lebih mirip dengan aslinya. Dalam bahasa Indonesiaseseorang yang mendalami bidang falsafah disebut "filsuf".
Kata falsafah atau filsafat dalam bahasa Indonesia merupakan kata serapan dari bahasa Arabفلسفة, yang juga diambil dari bahasa Yunani; Φιλοσοφία philosophia.Dalam bahasa ini, kata ini merupakan kata majemuk dan berasal dari kata-kata (philia= persahabatan, cinta dsb.) dan (sophia = "kebijaksanaan").Sehingga arti harafiahnya adalah seorang “pencinta kebijaksanaan”. Kata filosofi yang dipungut dari bahasa Belanda juga dikenal di Indonesia.Bentuk terakhir ini lebih mirip dengan aslinya. Dalam bahasa Indonesiaseseorang yang mendalami bidang falsafah disebut "filsuf".
Sabtu, 24 Mei 2014
Materi Pembelajaran Matematika Kelas X
Berikut adalah file pembelajaran kelas X yang dapat download :
| 10_matematika_buku_siswa.pdf |
| modul_eksponen.docx |
| modul_logaritma.docx |
| modul_pers._kuadrat.docx |
| modul_logika.docx |
| exponents.ppt |
| ppt_bahan_ajar_bentuk_akar.ppt |
| 02.logaritma.ppt |
| bab_1_pertidaksamaankuadrat.ppt |
| sistem-persamaan-linier.ppt |
Cerita Motivasi
Inspiring: Last homework from The Teacher
DREAMERSRADIO.COM - Kisah nyata ini datang dari Jepang, sosok guru selain memberikan pelajaran akademis juga ikut memberikan pendidikan. Guru istimewa ini mampu merasakan kalau waktunya hidup didunia tak lama lagi, sehingga ia menulis pekerjaan rumah terakhir bagi muridnya yang membuat orang terharu.
Sebelum guru tersebut menghembuskan nafas terakhir, dirinya masih sempat menuliskan PR untuk para siswanya. Jika umumnya para murid malas mengerjakannya, maka PR yang satu ini membuat para siswanya menangis.
Sebelum guru tersebut menghembuskan nafas terakhir, dirinya masih sempat menuliskan PR untuk para siswanya. Jika umumnya para murid malas mengerjakannya, maka PR yang satu ini membuat para siswanya menangis.
Sekilas SMAN Titian Teras Jambi
SMA Titian Teras Jambi diresmikan berdirinya pada tanggal 14 Juli 1994 oleh Gubernur Jambi ketika itu dijabat oleh Bapak H. Abdurrahman Sayoeti. Awalnya SMA Titian Teras berlokasi di Kecamatan Kota Baru Kota Jambi, namun pada tahun 1996 SMA Titian Teras pindah ke gedung baru yang berlokasi di Kelurahan Pijoan, Kecamatan Jambi Luar Kota Kabupaten Muaro Jambi berdiri di atas lahan seluas 12 ha. SMA Titian Teras dalam pengolahannya di bawah Yayasan Pendidikan Jambi yang diketuai oleh Bapak H. Abdurrahman Sayoeti.
Seragam Resmi SMAN TT HAS JAMBI
Jumat, 23 Mei 2014
Barisan dan Deret Aritmatika
Jumpa lagi dengan rumus matematika, dalam kesempatan ini kira-kira materi apa yang akan kita bahas? Sebelumnya telah kita pelajari bersama tentang materi turunan,
dan mudah-mudahan sobat semua telah paham tentang materi tersebut. Nah
bagaimana kalau sekarang kita pelajari tentang barisan dan deret
aritmatika, apa itu barisan dan deret aritmatika?

BARISAN ARITMATIKA
Pertama kita mulai dari barisan, barisan bilangan
adalah urutan dari bilangan yang dibuat berdasarkan aturan tertentu.
Sedangkan untuk barisan aritmatika adalah sebuah barisan bilangan dimana
setiap pasangan suku-suku yang berurutan memiliki selisih yang sama.
contoh : 6,9,12,15,…
Selisih bilangan
pada barisan aritmatika disebut beda yang biasa disimbolkan dengan
huruf b, untuk contoh diatas memiliki nilai beda 3. Dan bilangan yang
menyusun suatu barisan disebut suku, dimana suku ke n dari suatu barisan
disimbolkan dengan Un sehingga untuk suku ke 5 dari suatu barisan biasa disebut dengan U5. Khusus untuk suku pertama dari suatu barisan biasa disimbolkan dengan huruf a.
Jadi bentuk umum untuk suatu barisan aritmatika yaitu U1,U2,U3, … ,Un-1 atau a, a+b, a+2b, … , a+(n-1)b
Menentukan Rumus Suku ke-n suatu barisan
Pasangan suku-suku berurutan dari suatu barisan aritmatika mempunyai beda yang sama, maka
U2 = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
Berdasarkan
pola tersebut, dapatkah sobat menentukan suku ke-7, suku ke-26 hingga
suku ke-90? Dengan menggunakan pola diatas kita dapat mengetahui dengan
mudah suku-suku tersebut.
U7 = a + 6b
U26 = a + 25b
U90 = a + 89b
U26 = a + 25b
U90 = a + 89b
Sehingga berdasarkan runtutan penjelasan diatas untuk suku ke-n dapat kita peroleh menggunakan rumus :
Un = a + (n – 1)b, untuk n bilangan asli
DERET ARITMATIKA
Yang
dimaksud dengan deret aritmatika adalah penjumlahan dari semua anggota
barisan aritmatika secara berurutan. Contoh dari deret aritmatika yaitu 7
+ 10 + 13 + 16 + 19 + …
Misalnya
kita ambil n suku pertama, jika kita ingin menentukan hasil dari deret
aritmatika sebagai contoh untuk 5 suku pertama dari contoh deret diatas.
Bagaimana caranya?
7 + 10 + 13 + 16 + 19 = 65
Nah
untuk 5 suku pertama, masih mungkin kita menghitung manual seperti
diatas. Seandainya kita akan menentukan jumlah dari 100 suku pertama,
apakah masih mungkin kita menghitung manual seperti itu. Walaupun bisa
tetapi pastinya akan memakan waktu yang cukup lama. Nah kali ini akan
kita tunjukkan cara menentukannya, sebagai contohnya untuk mennetukan
jumlah 5 suku pertama dari contoh diatas.
Misalkan S5=7 + 10 + 13 + 16 + 19, sehingga

Walaupun dengan cara yang berbeda tetapi menunjukkan hasil yang sama yaitu 65. Perhatikan bahwa S5
tersebut dapat dicari dengan mengalikan hasil penjumlahan suku pertama
dan suku ke-5, dengan banyaknya suku pada barisan, kemudian dibagi
dengan 2. Analogi dengan hasil ini, jumlah n suku pertama dari suatu barisan dapat dicari dengan rumus berikut:
Sn = (a + Un) × n : 2
Dikarenakan Un = a + (n – 1)b, sehingga rumus di atas menjadiSn = (2a + (n – 1)b) × n : 2
SISIPAN DAN DERET ARITMATIKA
Sisipan
pada deret aritmatika yaitu menambahkan beberapa buah bilangan diantara
dua suku yang berurutan pada suatu deret aritmatika sehingga diperoleh
deret aritmatika yang baru. Sebagai contoh :
Deret mula-mula = 4 + 13 + 22 + 31 +……
Setelah disisipi = 4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28 + 31 +……
Untuk beda dari deret baru ini biasanya dinyatakan dengan b1, dapat ditentukan dengan rumus berikut :
b1 = b/(k+1)
b1 = beda deret baru
b = beda deret mula-mula
k = banyak bilangan yang disisipkan
Logika Matematika
A. Pernyataan
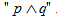
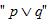 .
.
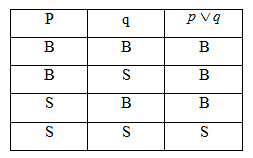
(iii) Implikasi
Implikasi “jika p maka q” dilambangkan dengan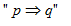 .
.
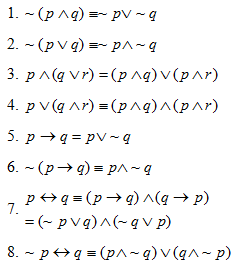

Yang
dimaksud dengan kalimat atau pernyataan adalah kalimat yang mempunyai
nilai benar atau salah, tetapi tidak sekaligus benar dan salah.
Ada dua jenis kalimat matematika, yaitu :
Kalimat tertutup, merupakan pernyataan yang nilai kebenarannya sudah pasti.
Contoh :
a) 3 x 4 = 12 (pernyataan tertutup yang benar)
b) 3 + 4 = 12 (pernyataan tertutup yang salah)
Kalimat terbuka, merupakan pernyataan yang kebenarannya belum pasti.
Contoh :
a : Ada daun yang berwarna hijau
b : Gula putih rasanya manis
B. Ingkaran Pernyataan
Ingkaran
atau negasi suatu pernyataan adalah pernyataan yang menyangkal
pernyataan yang diberikan. Ingkaran suatu pernyataan dapat dibentuk
dengan menambah “Tidak benar bahwa ...” di depan pernyataan yang
diingkar. Ingkaran pernyataan adalah ~ p.
Contoh :
Misalkan pernyataan p : Tembakau yang mengandung nikotin.
Ingkaran penyataan p adalah ~ p. Tidak benar bahwa tembakau mengandung nikotin.
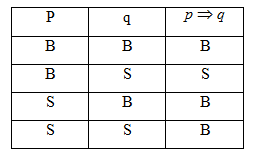
Tabel kebenaran dari ingkaran
C. Pernyataan Majemuk
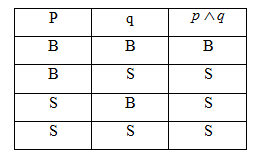
(i) Konjungsi
Pernyataan
p dengan q dapat digabung dengan kata hubung logika “dan” sehingga
membentuk pernyataan majemuk “p dan q” yang disebut konjungsi. Konjungsi
“p dan q” dilambangkan dengan 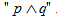

(ii) Disjungsi
Pernyataan
p dengan q dapat digabung dengan kata hubung logika “atau” sehingga
membentuk pernyataan majemuk “p atau q” yang disebut disjungsi.
Disjungsi p atau q dilambangkan dengan 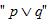 .
.

(iii) Implikasi
Implikasi “jika p maka q” dilambangkan dengan
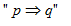 .
.

(iv) Biimplikasi
D. Ekuivalensi Pernyataan – Pernyataan Majemuk
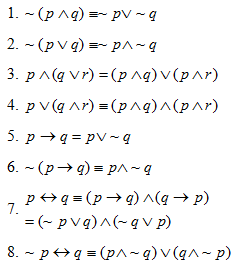
E. Konvers, Invers, dan Kontraposisi
Dari sebuah implikasi dapat diturunkan pernyataan yang disebut konvers, invers dan kontraposisi dari implikasi tersebut.

Peluang Matematika
A. Kaidah Pencacahan
I. Kaidah Perkalian
Kaidah perkalian mengatakan bahwa jika tempat pertama dapat diisi dengan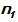 cara yang berbeda, tempat kedua dengan
cara yang berbeda, tempat kedua dengan 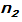 cara, …., tempat ke-k dengan
cara, …., tempat ke-k dengan 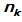 cara, maka banyaknya cara untuk mengisi tempat k yang tersedia adalah ….
cara, maka banyaknya cara untuk mengisi tempat k yang tersedia adalah …. 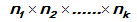
Contoh:
Bila kita perhatikan nomor rumah yang terdiri atas dua angka, tanpa angka nol, maka banyak rumah yang dimaksud dengan nomor ganjil ialah ….Jawab: Nomor rumah yang dimaksud terdiri atas dua angka. Ini berarti ada dua tempat yang harus diisi, yaitu PULUHAN dan SATUAN. Karena nomor harus ganjil, maka tempat satuan hanya dapat diisi oleh bilangan-bilangan ganjil, yaitu 1, 3, 5, 7, dan 9. Dengan demikian ada 5 cara untuk mengisi tempat satuan, sehingga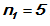
Sedangkan tempat puluhan dapat diisi oleh angka 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Sehingga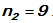 Dengan demikian banyaknya rumah dengan nomor ganjil adalah :
Dengan demikian banyaknya rumah dengan nomor ganjil adalah :
II. Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga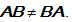
Permutasi k unsur dari n unsur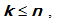 adalah semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis
adalah semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis 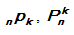 atau
atau 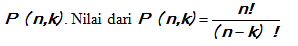 .
.
Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Contoh :
Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6 unsur yaitu :
III. Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur dapat disusun himpunan bagiannya dengan untuk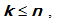 Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan ,
Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan , 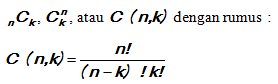
Contoh :
Diketahui himpunan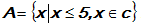 .
.
Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :
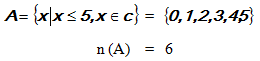
Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).
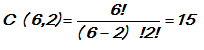
B. Peluang Suatu Kejadian
1. Pengertian Ruang Sampel dan Kejadian
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S.
Contoh:
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG} P = {AAG, AGA, GAA}
Kaidah-kaidah pencacahan mencoba menemukan beberapa banyaknya hasil yang mungkin terjadi (muncul) pada berbagai percobaan.
Secara umum cara menemukan banyaknya hasil yang mungkin muncul pada
suatu percobaan adalah dengan menggunakan pendekatan-pendekatan sebagai
berikut :
1. Kaidah Perkaian
2. Permutasi
3. Kombinasi
1. Kaidah Perkaian
2. Permutasi
3. Kombinasi
I. Kaidah Perkalian
Kaidah perkalian mengatakan bahwa jika tempat pertama dapat diisi dengan
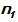 cara yang berbeda, tempat kedua dengan
cara yang berbeda, tempat kedua dengan 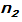 cara, …., tempat ke-k dengan
cara, …., tempat ke-k dengan 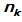 cara, maka banyaknya cara untuk mengisi tempat k yang tersedia adalah ….
cara, maka banyaknya cara untuk mengisi tempat k yang tersedia adalah …. 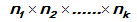
Contoh:
Bila kita perhatikan nomor rumah yang terdiri atas dua angka, tanpa angka nol, maka banyak rumah yang dimaksud dengan nomor ganjil ialah ….Jawab: Nomor rumah yang dimaksud terdiri atas dua angka. Ini berarti ada dua tempat yang harus diisi, yaitu PULUHAN dan SATUAN. Karena nomor harus ganjil, maka tempat satuan hanya dapat diisi oleh bilangan-bilangan ganjil, yaitu 1, 3, 5, 7, dan 9. Dengan demikian ada 5 cara untuk mengisi tempat satuan, sehingga
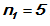
Sedangkan tempat puluhan dapat diisi oleh angka 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Sehingga
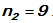 Dengan demikian banyaknya rumah dengan nomor ganjil adalah :
Dengan demikian banyaknya rumah dengan nomor ganjil adalah :
II. Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga
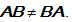
Permutasi k unsur dari n unsur
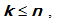 adalah semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis
adalah semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis 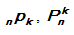 atau
atau 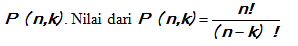 .
.
Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Contoh :
Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6 unsur yaitu :
III. Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur dapat disusun himpunan bagiannya dengan untuk
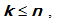 Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan ,
Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan , 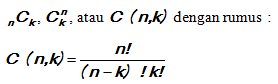
Contoh :
Diketahui himpunan
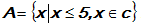 .
.
Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :
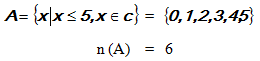
Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).
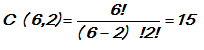
B. Peluang Suatu Kejadian
1. Pengertian Ruang Sampel dan Kejadian
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S.
Contoh:
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG} P = {AAG, AGA, GAA}
2. Pengertian Peluang Suatu Kejadian
Pada
suatu percobaan terdapat n hasil yang mungkin dan masing-masing
berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k
hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A ) ditentukan dengan rumus : 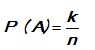 Contoh :
Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3
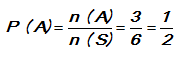
3. Kisaran Nilai Peluang
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan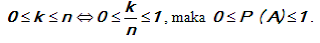
Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti.
4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ).
Contoh :
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga :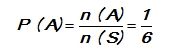
Frekuensi harapan munculnya mata dadu 1 adalah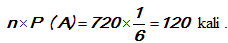
5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga :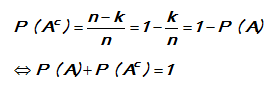
Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).
C. Peluang Suatu Kejadian Majemuk
1. Gabungan Dua Kejadian
Untuk setiap kejadian A dan B berlaku :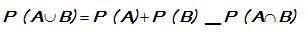
Catatan :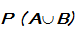 dibaca “ Kejadian A atau B dan
dibaca “ Kejadian A atau B dan 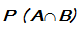 dibaca “Kejadian A dan B”
dibaca “Kejadian A dan B”
Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :
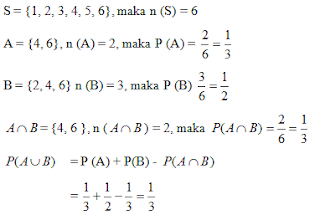
2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku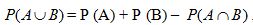 Jika
Jika 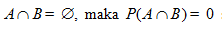 . Sehingga
. Sehingga 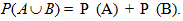 Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
3. Kejadian Bersyarat Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika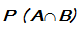 adalah peluang terjadinya A dan B, maka
adalah peluang terjadinya A dan B, maka 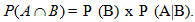 Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :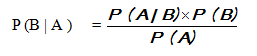
5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga: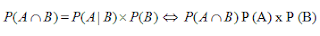
D. Sebaran Peluang
1. Pengertian Peubah acak dan Sebaran Peluang.
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap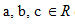 dan setiap
dan setiap 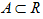 maka:
maka:

Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut :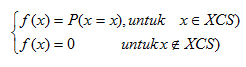
2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :
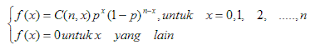
Dengan P sebagai parameter dan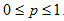
Rumus ini dinyatakan sebagai:
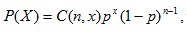 untuk n = 0, 1, 2, .... ,n
Dengan P sebagai parameter dan
untuk n = 0, 1, 2, .... ,n
Dengan P sebagai parameter dan 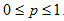
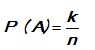 Contoh :
Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3
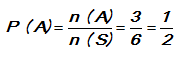
3. Kisaran Nilai Peluang
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan
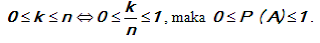
Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti.
4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ).
Contoh :
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga :
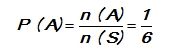
Frekuensi harapan munculnya mata dadu 1 adalah
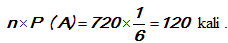
5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga :
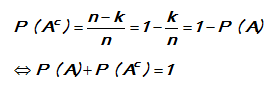
Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).
C. Peluang Suatu Kejadian Majemuk
1. Gabungan Dua Kejadian
Untuk setiap kejadian A dan B berlaku :
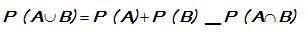
Catatan :
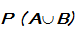 dibaca “ Kejadian A atau B dan
dibaca “ Kejadian A atau B dan 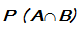 dibaca “Kejadian A dan B”
dibaca “Kejadian A dan B”
Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :
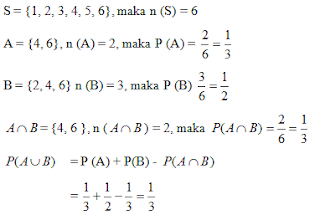
2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku
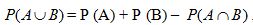 Jika
Jika 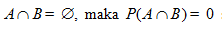 . Sehingga
. Sehingga 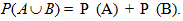 Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
3. Kejadian Bersyarat Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika
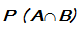 adalah peluang terjadinya A dan B, maka
adalah peluang terjadinya A dan B, maka 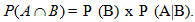 Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :
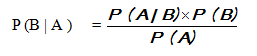
5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga:
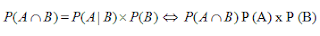
D. Sebaran Peluang
1. Pengertian Peubah acak dan Sebaran Peluang.
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap
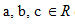 dan setiap
dan setiap 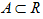 maka:
maka:

Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut :
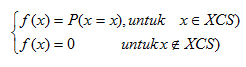
2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :
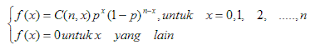
Dengan P sebagai parameter dan
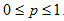
Rumus ini dinyatakan sebagai:
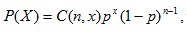 untuk n = 0, 1, 2, .... ,n
Dengan P sebagai parameter dan
untuk n = 0, 1, 2, .... ,n
Dengan P sebagai parameter dan 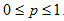
P = Peluang sukses
n = Banyak percobaan
x = Muncul sukses
n-x = Muncul gagal
Langganan:
Komentar (Atom)











